Sobre mi

INTERESES Y GUSTOS:
Estudiante de la carrera Matemáticas Aplicadas y Computación de la FES Acatlán, me gusta escuchar música, bailar y pasar tiempo con las personas que quiero, visitar museos y caminar en parques.
biografias
linea de tiempo
https://www.timetoast.com/timelines/1815635
Más informaciónConceptos “Paradigma de Ackoff”
CONCEPTOS | IDEAS BÁSICAS |
CAUSA Y EFECTO | Una cosa es la causa de otra, su efecto, si la causa es tanto necesaria como suficiente para su efecto. Una cosa en necesaria para otra si la segunda no puede ocurrir a menos que ocurra la primera. Una cosa es suficiente para otra si la ocurrencia de la primera segura la ocurrencia de la segunda. |
ADAPTACIÓN | Ajustar una cosa a otra. |
ERA
| Periodo de la historia en el que la gente comparte, el uso de un método común de investigación y una visión de la naturaleza del mundo que se deriva del mismo. |
PINTURA | Su función en la Edad Media era ayudar al hombre a ganar su salvación en la otra vida. |
ERA DE LA MÁQUINA | Creada a partir de dos creencias: que el universo era una máquina creada por Dios para realizar su obra y que él había creado al hombre a su imagen y semejanza. |
RENACIMIENTO | Nuevo despertar o volver a nacer. |
ANÁLISIS | Método básico de investigación de la era iniciada por el Renacimiento. |
REDUCCIONISMO | Doctrina que afirma la creencia de que toda realidad de nuestra experiencia del mundo puede reducirse a elementos indivisibles fundamentales. |
MECANICISTA | El concepto del universo que se deriva del uso exclusivo del análisis y de las doctrinas del reduccionismo y el determinismo. |
SISTEMA | Un todo que no puede dividirse en partes independientes. |
ORGANIZACIÓN | Entidad biológica concentrada en un solo propósito. |
CRECER | Aumentar en tamaño o número. |
DESARROLLARSE | Aumentar la habilidad y el deseo de uno mismo para satisfacer las necesidades y los deseos legítimos tanto propios como los de los demás. |
DETERMINISTAS | Los sistemas y modelos en los que ninguna de las partes ni el todo son intencionados. |
ANIMADOS | Los sistemas y modelos en los que el todo es intencionado, pero las partes no. |
SOCIALES | Los sistemas y modelos en los que tanto las partes como el todo son intencionados. |
AUTOMATIZACIÓN | Reemplazo de la mente. |
MECANIZACIÓN | Reemplazo del músculo. |
DATOS | Símbolos que representan las propiedades de objetos o eventos. |
ORGANIZACIÓN DE UN SISTEMA | Dividir su funcionalidad de trabajo entre sus partes y tomar las medidas necesarias para su coordinación. |
PERSPECTIVA TELEOLÓGICA | Orientada a resultados. |
ORGANISMOS INTENCIONALES | Cuyas partes tienen funciones pero no finalidades por sí mismas. |
ORGANIZACIÓN DEMOCRÁTICA | Aquella en la que los miembros tienen libertad y oportunidades considerables para hacer elecciones. |
CHOQUE DEL FUTURO | Parálisis frente al cambio que requiere modificaciones. |
ANÁLISIS | Inferir cómo funcionan las partes e intentar extraer una comprensión del todo. |
Mapa Paradigma de Ackoff
BIBLIOGRAFIA
- RUSSELL L. ACKOFF. (2007). EL PARADIGMA DE ACKOFF: UNA ADMINISTRACIÓN SISTÉMICA. Spanish: Editorial Limusa S.A. De C.V.; Tra edition.
IMAGENES
- GUEST BLOGGER. (Oct 02). 6 PASOS PARA EL BUEN ANÁLISIS DE DATOS. 2018, de BID Sitio web: https://blogs.iadb.org/abierto-al-publico/2014/10/02/6-pasos-para-el-buen-analisis-de-datos/
- power data. (2016). ¿Qué es la auditoría de base de datos?. 2018, de power datos Sitio web: https://blog.powerdata.es/el-valor-de-la-gestion-de-datos/que-es-la-auditoria-de-base-de-datos
Infografía
Tipos de solución en la programación lineal
Tipos de solución en la programación lineal
E-book modelos lineales
Cuadro conceptos Métodos de Solución
| CONCEPTO | CARACTERÍSTICA DEL CONCEPTO |
| ALGORITMO SIMPLEX | Busca el óptimo de un problema de P.L. recorriendo sólo algunos de los vértices del poliedro que representa el conjunto de soluciones factibles.
1. Convierta el modelo PL a su forma estándar. 2. Obtenga una SBF a la forma estándar. 3. Determine si la SBF es óptima: Si hay una variable no básica cuyo aumento hace que el valor actual de la función a maximizar suba, entonces la solución actual no es óptima. 4. Si la SBF no es óptima, determine la variable no-básica que debería convertirse en básica (la de mayor impacto en la función objetivo) y cual variable básica debería convertirse en una no-básica (la que impone una restricción mayor a la variable de mayor impacto). Con la selección anterior y usando operaciones elementales de renglón determine una SBF nueva adyacente a la anterior. 5. Reinicie con el paso 3 con la nueva SBF |
| EMPATE EN VARIABLE DE ENTRADA | Cuando se produce un empate en la condición de decisión de la variable entrante se puede optar por cualquiera de ellas sin que esto afecte a la solución final. Por contra si influye en el número de iteraciones necesarias para obtener dicha solución. Se aconseja optar a favor de las variables básicas ya que ellas son las que formarán parte de la solución óptima. |
EMPATE EN VARIABLE DE SALIDA | Se puede nuevamente optar por cualquiera de ellas. Sin embargo, a fin de no alargar el problema y evitar la entrada en un bucle infinito (caso degenerado), se discrimina a favor de las variables de decisión haciendo que permanezcan en la base. |
EQUIVALENCIAS | REGLAS DE EQUIVALENCIA:
|
FORMA AUMENTADA | Cuando el origen no pertenece a la solución inicial se agregan variables artificiales, estas sólo se agregan en las restricciones que no contienen variables de holgura, a este modelo se le conoce como forma aumentada. |
FORMA CANÓNICA | Un problema de P.L. está en la forma canónica si para un problema de:
|
| FORMA ESTANDAR | Un modelo de PL se dice que está en su forma estándar si cada restricción es una igualdad y las restricciones de signo para cada variable son del tipo mayor o igual que cero. M ecuaciones con N incógnitas (incluye variable de holgura y/o exceso) |
MÉTODO DE LAS DOS FASES | El Método de las Dos Fases es una variante del Algoritmo simplex, que es usado como alternativa al Método de la M grande, donde se evita el uso de la constante M para las variables artificiales. FASE 1. Formule un nuevo problema reemplazando la función objetivo por la suma de las variables artificiales. La nueva función objetivo se minimiza sujeta a las restricciones del problema original. Si el problema tiene un espacio factible el valor mínimo de la función objetivo óptima será cero, lo cual indica que todas las variables artificiales son cero. En este momento pasamos a la fase 2. * Si el valor mínimo de la función objetivo óptima es mayor que cero, el problema no tiene solución y termina anotándose que no existen soluciones factibles. FASE 2. Utilice la solución óptima de la fase 1 como solución de inicio para el problema original. En este caso, la función objetivo original se expresa en términos de las variables no básicas utilizando las eliminaciones usuales Gauss-Jordan. |
MÉTODO M GRANDE | El método M grande comienza con la programación lineal en forma de ecuación. Una ecuación i que no tenga una holgura (o una variable que pueda hacer el papel de una holgura). Se aumenta con una variable artificial, A1, para formar una solución básica con todas las holguras. Sin embargo, como las variables artificiales son ajenas al modelo de programación lineal. Se usa un mecanismo de retroalimentación en el que el proceso de optimización trata en forma automática de hacer que esas variables tengan un nivel cero. En otras palabras, la solución final será como si las variables artificiales nunca hubieran existido en primer lugar. El resultado deseado se obtiene penalizando las variables artificiales en la función objetivo. Pasos: 1. Se debe llevar a la forma estándar cambiando cada restricción por una igualdad. 2. Se debe Penalizar la Función Objetivo 3. Antes de pasar al paso inicial debemos a cada restricción que posea una variable inicial, se debe multiplicar por M y sumarla con a la función objetivo. 4. Crear la tabla con la función objetivo resultante. 5. Aplicar el método Simplex Conocido (iterar por Gauss Jordan). |
| OPTIMALIDAD | En problemas de maximización, el P.L. es óptimo si todos los costes reducidos ( son menores o iguales que cero. En problemas de minimización cada coste reducido debe ser mayor o igual que cero. |
| SOLUCIÓN BÁSICA | Es aquella que tiene al menos n-m componentes nulos o variables no básicas, el resto de las variables (m) se resuelven con sistema de ecuaciones. |
| SOLUCIÓN BÁSICA FACTIBLE | Todas las variables básicas son mayores o iguales que cero y n-m valen 0 (puntos extremos de la región factible) |
VARIABLE ARTIFICIAL | Una variable artificial es un truco matemático para convertir inecuaciones "≥" en ecuaciones, o cuando aparecen igualdades en el problema original, la característica principal de estas variables es que no deben formar parte de la solución, dado que no representan recursos. Estas variables se representan por la letra "A", siempre se suman a las restricciones. |
VARIABLE DE ENTRADA | Se refiere a la variable no básica en el renglón “z” con el coeficiente más negativo, si se trata de una maximización, o el coeficiente más positivo, si se trata de una minimización que en el siguiente punto adyacente se convierte en variable básica. |
| VARIABLE DE EXCESO | Son variables que se restan en las restricciones con signo ≥ |
| VARIABLE DE HOLGURA | Son variables que se suman en las restricciones con signo ≤ |
VARIABLE DE SALIDA | Variable básica asociada con la mínima razón no negativa con el coeficiente más negativo, si se trata de una maximización, o el coeficiente más positivo, si se trata de una minimización, la cual, en la tabla de solución siguiente, pasará a ser variable no básica. |
VARIABLES BÁSICAS | Variable de decisión que se conserva dentro del nuevo sistema y se utiliza para resolverlo. |
| VARIABLES NO BÁSICAS | Variable de decisión que deliberadamente se hace cero. |
| VARIABLES NO RESTRINGIDAS | Algunas veces las variables de decisión pueden tomar cualquier valor real. Xi s.r.s Cambio de variable Xi = Ui – Vi Ui …. Parte positiva de Xi Vi …. Parte negativa de Xi |
REFERENCIAS
- PHPSimplex. (s.f.). Teoría del método Simplex. Recuperado 2 octubre, 2018, de http://www.phpsimplex.com/teoria_metodo_simplex.htmx
- Programación Lineal: Método Simplex. (s.f.). Recuperado 2 octubre, 2018, de http://cmapspublic.ihmc.us/rid=1J9ZKR3C6-MQNT0K-166/PROGRAMACI%C3%93N%20LINEAL%20Metodo%20Simplex.pdf
- Collazo Pedraja, A. R. (2018, 29 abril). APUNTES SOBRE EL MÉTODO SÍMPLEX DE PROGRAMACIÓN LINEAL. Recuperado 2 octubre, 2018, de http://cicia.uprrp.edu/publicaciones/docentes/metodosimplexdePL.pdf
- Método Simplex. (s.f.). Recuperado 2 octubre, 2018, de https://www.ingenieriaindustrialonline.com/herramientas-para-el-ingeniero-industrial/investigaci%C3%B3n-de-operaciones/m%C3%A9todo-simplex/
- Martínez, H., & Celis, R. (s.f.-b). FORMA CANONICA Y FORMA ESTANDAR. Recuperado 2 octubre, 2018, de http://hemaruce.angelfire.com/FORMA_CANONICA_Y_FORMA_ESTANDAR.pdf
- Guzmán, R., Montaño, P., & Noriega, R. (2012, 10 julio). M grande. Recuperado 2 octubre, 2018, de https://es.slideshare.net/rafarngt/m-grande
- METODO DE LAS DOS FASES.. (s.f.). Recuperado 2 octubre, 2018, de http://www.itlalaguna.edu.mx/academico/carreras/industrial/invoperaciones1/U2D.html
Ejercicios métodos de solución
| EJERCICIO | RESPUESTA |
| MÉTODO SIMPLEX DE LAS DOS FASES Min z=80X1 + 124X2 s.a: X1 + 0.8X2 ≥ 100 X1 + 2X2 ≥ 200 X1, X2 ≥ 0 | 1) Min z=0X1 + 0X2 + 0H1 + 0H2 + 1A1 + 1A2 s.a X1 + 0.8X2 - H1 + A1 = 100 X1 + 2X2 - H2 + A2 = 200 X1, X2, H1, H2, A1, A2 ≥ 0 Donde H es una variable de holgura y A una variable artificial. PRIMERA FASE TABLA 1 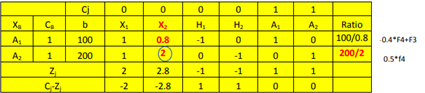 · ·
Una vez que hemos llenado la tabla procedemos a realizar el proceso de optimización (1ra. Fase) para lo cual se debe: -0.4*F4+F3 0.5*f4
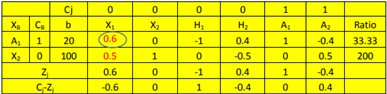 ITERACIÓN 2
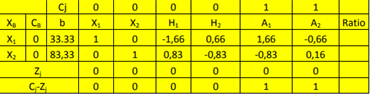 Vemos los Cj-Zj de la tabla 3 y vemos que no hay ningún valor menor que cero, es decir que todos los Cj-Zj ≥ 0. Por lo que hemos llegado al fin de la 1ra. Fase. Esto nos permite pasar a la 2da. Fase. Vemos los Cj-Zj de la tabla 3 y vemos que no hay ningún valor menor que cero, es decir que todos los Cj-Zj ≥ 0. Por lo que hemos llegado al fin de la 1ra. Fase. Esto nos permite pasar a la 2da. Fase.SEGUNDA FASE
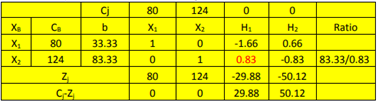 Observamos la sexta fila y buscamos los Cj – Zj ≥0 por lo que hemos llegado al óptimo.Por lo que la solución óptima será: X1=33.33 X2=83.33 Z=80*33.33 + 124*83.33= 12,999.32=13,000 |
MÉTODO SIMPLEX  |
S.A 4X1 + 2X2 + S1 = 16 (Ecuación 1) 8X1 + 8X2 + S2 = 16 (Ecuación 2) 2X2 + S3 = 10 (Ecuación 3) X1, X2, 0S1, 0S2, 0S3>= 0
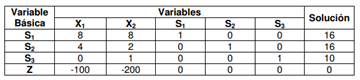
Razón Menor = Fila perteneciente a S1 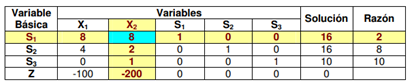
 La nueva tabla Simplex: 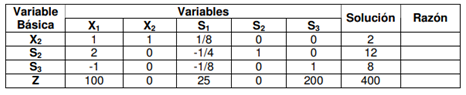 Como no hay más iteraciones debido a que no existen coeficientes de Z negativos en la nueva tabla el valor máximo se alcanza para: X2 = 2 Z = 400. |
Bibliografía:
Prof.: MSc. Julio Rito Vargas Avilés. . (Octubre 2012). MÉTODO SIMPLEX DE LAS DOS FASES. octubre2018, de Julio Rito Vargas Avilés. Sitio web: https://jrvargas.files.wordpress.com/2008/08/ejemplo-mc3a9todo-simplex-de-las-dos-fases.pdf
Juan Carlos Vergara Schmalbach. (--). EJERCICIOS RESUELTOS INVESTIGACIÓN DE OPERACIONES. octubre 2018, de Juan Carlos Vergara Schmalbach Sitio web: http://juancarlosvergara.50webs.org/Apuntes/Ejercicios%20Resueltos%201,%20Metodo%20grafico%20y%20simplex.pdf
